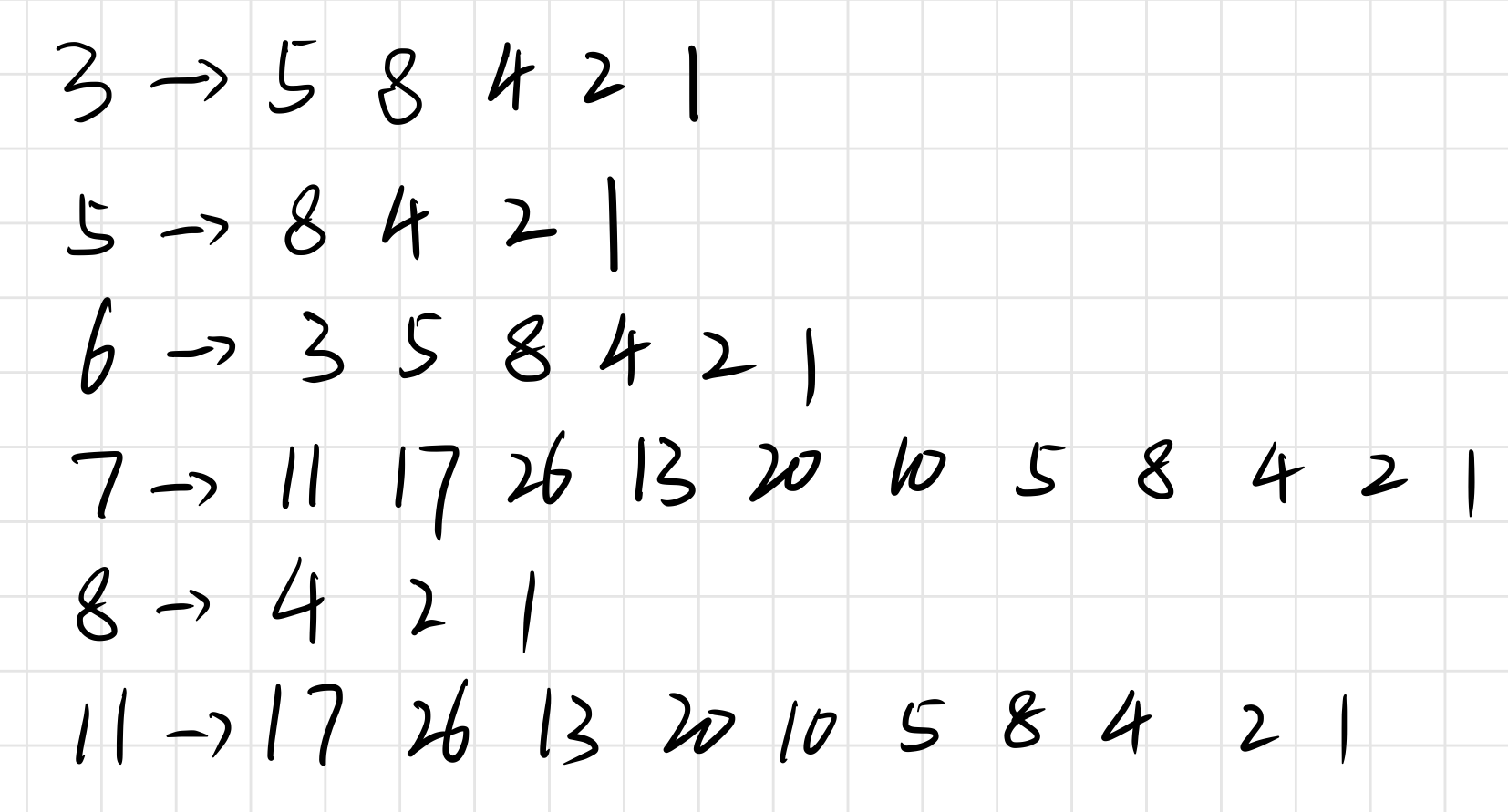1005 继续(3n+1)猜想 (25分)

卡拉兹(Callatz)猜想已经在1001中给出了描述。在这个题目里，情况稍微有些复杂。

当我们验证卡拉兹猜想的时候，为了避免重复计算，可以记录下递推过程中遇到的每一个数。例如对 n=3 进行验证的时候，我们需要计算 3、5、8、4、2、1，则当我们对 n=5、8、4、2 进行验证的时候，就可以直接判定卡拉兹猜想的真伪，而不需要重复计算，因为这 4 个数已经在验证3的时候遇到过了，我们称 5、8、4、2 是被 3“覆盖”的数。我们称一个数列中的某个数 n 为“关键数”，如果 n 不能被数列中的其他数字所覆盖。

现在给定一系列待验证的数字，我们只需要验证其中的几个关键数，就可以不必再重复验证余下的数字。你的任务就是找出这些关键数字，并按从大到小的顺序输出它们。

输入格式：

每个测试输入包含 1 个测试用例，第 1 行给出一个正整数 K (<100)，第 2 行给出 K 个互不相同的待验证的正整数 n (1<n≤100)的值，数字间用空格隔开。

输出格式：

每个测试用例的输出占一行，按从大到小的顺序输出关键数字。数字间用 1 个空格隔开，但一行中最后一个数字后没有空格。

输入样例：

1
2
6
3 5 6 7 8 11

输出样例：

1
7 6

思路：

这题和1003一样，主要难度在于读懂题目意思。先抛开题目，我们先看看输入样例里面的六个数在进行(3n+1)猜想时需要算的数字。

vP56pQ.png

其中我们可以看到很多重复的数字，出现频率最高的就是5、8、4、2、1这几个数字了。我们这个时候再回看题目就会很好理解了。 为了避免重复计算 ，我们就把上图中这些计算过程中出现的数字打上一个 “覆盖” 的标签，所谓“关键数”呢， 其实就是这些计算过程中“暂时”还没出现的数字 ，比如说上图中的 6和7 ，这也就是这道题的答案了。
同样的也是要记录某一个数据的状态，这里我用到 map容器 ，利用<int,bool>的对组，把输入进去的数字标记为 “true” ，因为还没有进行计算前，这些数字都要从头算起，true和false就能很自然的代表是否是关键数。在“砍”的过程中，出现一个新的数字，那这个数字就相当于已经计算过了，将它设为 “false” ，循环计算后依然为 “true” 的数字就是关键数了。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
using namespace std;

int main()
{
    int n;
    cin >> n;

    int num;
    map<int, bool> m; //int为输入的数字 bool为该数字的状态
    vector<int> v;
    for (int i = 0; i < n; i++)
    {
        cin >> num;
        m[num] = true; //还没开始计算，全部设为true
    }

    for (map<int, bool>::iterator it = m.begin(); it != m.end(); it++)
    {
        //开始循环计算每个数字，计算过程中出现过的数字全部设为false
        int temp = it->first;
        while (temp != 1)
        {
            if (temp & 1)
            {
                m[(temp * 3 + 1) / 2] = false;
                temp = (temp * 3 + 1) / 2;
            }
            else
            {
                m[temp / 2] = false;
                temp /= 2;
            }
        }
    }
    for (map<int, bool>::iterator it = m.end(); it != m.begin(); it--)
        //由于要从大到小输出关键数字，这里我利用排序将结果重新排列
    {
        if (it->second == true)
        {
            v.push_back(it->first);
        }
    }

    sort(v.begin(), v.end()); //默认从小到大排序

    for (int i = v.size() - 1; i >= 0; i--) //所以这里是反向打印
    {
        cout << v[i];
        if (i)
            cout << " ";
    }

    return 0;
}